Getting the type signature right was 99% of the work in implementing pluck and sculpt for HLists in Frunk.

Here’s what I’ve learnt along the way: what works, and what doesn’t work (and why).

As you may already know, Rust eschews the now-mainstream object-oriented model of programming (e.g. in Java, where behaviour for a type is added to the type/interface definition directly) in favour of a typeclass-like approach (e.g. in Haskell where you can ad-hoc add behaviour to a type separate from the type definition itself). Both approaches have their merits, and indeed, some languages, such as Scala, allow for a mix of both.

For those coming from the OOP school of programming, Rust’s system of adding behaviour to types might be daunting to come to grips with. At a glance, it might not be obvious how to get things done, especially when what you want to build goes beyond implementing Debug or Eq. If your abstraction has a certain degree of type-level recursiveness, it might be even harder to see the light at the end of the tunnel, and the lack of online material covering that sort of thing doesn’t help.

As a Scala guy with Haskell knowledge, I’m no stranger to typeclasses, but it took me a while and several failed attempts to figure out how to implement the following:

1. Plucking out a value by type from an HList and getting back the remainder **
2. Sculpting an HList into another shape, and getting back the remainder (in the case where we only want a smaller subset than the original) **

Of course, the type signature of the finished product can be intimidating !

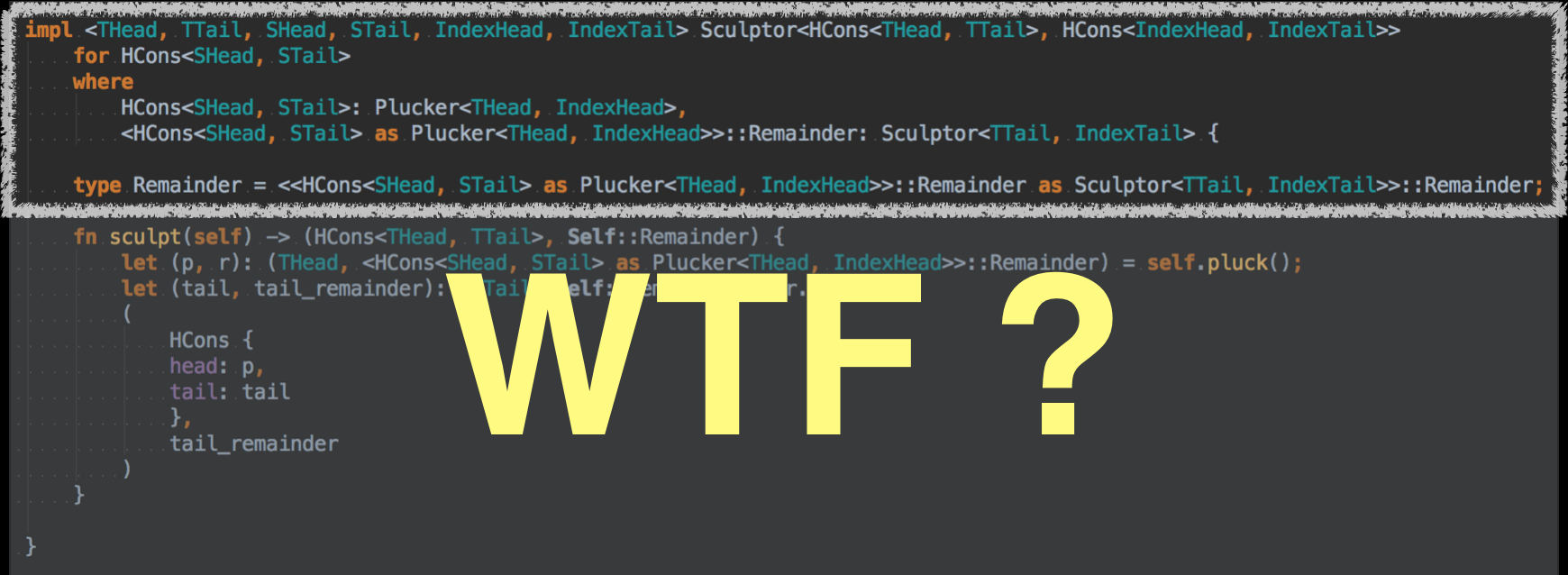
In this post, I’ll briefly introduce Rust’s trait system and present my mental model for writing trait implementations that deal with type-level recursion. To do so, I will go through how pluck() and sculpt() were written in Frunk, as well as recount some of my failed approaches so you can learn from my mistakes.

Hopefully, by the end of it, you’ll be able to look at signatures like the one above and not go “WTF”, but rather, “FTW”.

“Type-level recursion”?

Ok, I may be butchering/making up a term, but by “type-level recursion”, I’m referring to recursive expansions/evaluations of types at compile-time, particularly for the purpose of proving that a certain typeclass instance exists at a function call site. This is distinct from runtime “value”-level recursion that occurs when you call a function that calls itself.

If you’re having trouble understanding the difference:

• Value-level recursion: If it can’t find an exit condition, your program is stuck running forever.
• Type-level recursion: If it can’t expand/find the exit-type, your compiler will either give up or never finish compiling; you won’t even have a program to run.

Outline

• Basic Gist of Rust typeclasses (traits)
  • Dependent trait implementations
  • Mental model for type-level recursion
    • Recursion on the value level
    • Recursion on the type level
• What the Frunk?
• Plucking from HLists
  • Implementation intuition
  • First attempt
  • Second attempt
  • Type-level walkthrough
• Sculpting HLists
  • Implementation intuition
  • First attempt
  • Second attempt
• Conclusion
  • Credit

Basic Gist of Rust typeclasses (traits)

In Rust, typeclass is spelt trait, and although that word is somewhat ambiguous and overloaded with different meanings depending on context (e.g. in Scala), I’ll try to stick with it throughout this article. Subsequently, a typeclass instance is called an “implementation” (impl in code) in Rust.

Here is a basic example of a simple trait and implementation for a type Circle, taken from the official Rust book.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

// A trait that allows you to call "area" on something
trait HasArea {
    fn area(&self) -> f64;
}

// Our type
struct Circle {
    x: f64,
    y: f64,
    radius: f64,
}

// Our implementation of HasArea for Circle
impl HasArea for Circle {
    fn area(&self) -> f64 {
        std::f64::consts::PI * (self.radius * self.radius)
    }
}

For comparison, here is the Haskell equivalent

1
2
3
4
5
6
7
8
9
10

-- Our typeclass
class HasArea a where
  area :: a -> Float

-- Our type
data Circle = Circle { x :: Float, y :: Float, radius :: Float }

-- Our typeclass instance for Circle
instance HasArea Circle where
  area c = pi * radius c ^ 2

In both of these cases, what we see is

1. There is a trait, HasArea, which describes behaviour (must implement an area function that takes as its first argument the implementing type) for types that want to belong to, or join it.
2. Next, we have a type, Circle, which has one purpose: hold data.
3. Then, we add Circle to the HasArea trait by implementing an instance of the trait, fulfilling the contract by writing the area function.

The key difference between this approach and the OOP approach is that adding behaviour to an existing type does not require us to edit the original type declaration, nor does it require us to create a wrapper type. This allows us to add behaviour to types that do not belong to us (e.g. we don’t have access to its source)! This flexibility is a key advantage of the typeclass/trait approach. For a much more detailed comparison between OOP and typeclasses (traits), checkout this wiki entry on haskell.org.

Dependent trait implementations

Sometimes, you’ll want to write trait implementations for data types that have one or more type parameters. In these cases, your trait implementation will likely require that implementations of the trait exist for each of those type parameters.

For example

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44

// The Add trait, which exists in core::ops, copied verbatim here.
//
// Note that the Add trait has a right hand side (RHS) type parameter
// to represent the type that the implementing trait is being added
// with.
pub trait Add<RHS=Self> {
    /// The resulting type after applying the `+` operator
    #[stable(feature = "rust1", since = "1.0.0")]
    type Output;

    /// The method for the `+` operator
    #[stable(feature = "rust1", since = "1.0.0")]
    fn add(self, rhs: RHS) -> Self::Output;
}

// Our Cup struct. We signal that its contents can be
// anything because it has an unrestricted type parameter
// of A
struct Cup<A> {
    content: A,
}

// In our case, we want to implement Add<Cup<A>> because we want to add
// 2 cups with the same content type together, but we don't know in
// advance what kind of content would be in them; hence we keep
// it parameterised with A.
//
// Thus, we write an implementation of Cup for Add, but add a restriction:
// the implementation only exists for Cups where the content is bound to a
// type that is already implements the Add trait (thus "A: Add<A>")
impl<A: Add<A>> Add<Cup<A>> for Cup<A>
{
    // This is what is called an associated type.
    // Here, Output is the type that will be returned
    // from the add operation
    type Output = Cup<< A as Add<A> >::Output>;

    fn add(self, rhs: Cup<A>) -> Self::Output {
        // Here we make use of the Add trait for A to add
        // the contents from both cups together
        let added_content = self.content.add(rhs.content);
        Cup { content: added_content }
    }
}

Making Cup part of the Add typeclass will allow us to call cup_a + cup_b, which is kind of neat. One thing to take note of here is the Output associated type. Pay attention to the fact that in our implementation of Add for Cup, the type of Output is Cup<< A as Add<A> >::Output>, which means that ultimately, the output of Adding of 2 Cup<A>s will depend on what the Output of Add<A> is. The < A as Add<A> > part can be read as “summon the Add<A> implementation for the type A” (the compiler will do the actual lookup work here; if one doesn’t exist, your code will fail to compile), and the ::Output following it means “retrieve the associated type, Output, from that implementation”. Let this sink in, because it’s important in order for us to move towards the concept of type-level recursion for traits.

Here is another way to write the same thing: using where clause syntax, so that the restriction goes at the end of the initial type signature in our implementation declaration. This is useful when you have more than 2 or 3 type parameters for your typeclass instance and you have a complex set of restraints. Using where can help cut down on initial noise.

1
2
3
4
5
6
7
8
9
10

impl<A> Add<Cup<A>> for Cup<A>
    where A: Add<A>
{
    type Output = Cup<<A as Add<A>>::Output>;

    fn add(self, rhs: Cup<A>) -> Self::Output {
        let added_content = self.content.add(rhs.content);
        Cup { content: added_content }
    }
}

Here’s another, more general implementation of Add for Cup. It’s more general because it lets us add Cups of different content types, provided that there exists an Add<B> implementation for whatever concrete type is bound to A in any given Cup<A>.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

// Instead of just A, we introduce another type parameter, B, which
// is passed as the type parameter for the Cup that we want to add with
impl<A, B> Add<Cup<B>> for Cup<A>
    // This next line means "A must have an Add<B> implementation"
    where A: Add<B>
{
    // The Output associated type now depends on the Output of <A as Add<B>>
    type Output = Cup<<A as Add<B>>::Output>;

    fn add(self, rhs: Cup<B>) -> Self::Output {
        // Notice that we can use the operator "+"
        let added_content = self.content + rhs.content;
        Cup { content: added_content }
    }
}

Mental model for type-level recursion

By this point, we have covered most of the basic understanding required to write more complex traits and implementations. To recap, they are:

1. The differences between a trait, a type, and a trait implementation
2. How to use bounds (A: Add<A> or where clauses) when writing implementations for generic types
3. How to summon an implementation for a given type (<A as Display>)
4. How to write and use associated types (see Output in the above examples)

For a more thorough introduction to Rust’s trait system, by all means refer to the official Rust docs on traits.

Before going any further, I’d like to provide you with my mental model of how to think about recursion on the type level.

Recursion on the value level

You write a function that keeps calling itself until an exit condition is met, then returns a value.

Recursion on the type level

You write implementations of your trait for exit-types and work-to-be-done types. In order to prove an implementation of your trait exists for a concrete type at a function call site, the compiler will try to lookup and expand/expand types recursively until it can figure out a concrete implementation to use, or gives up with an error.

This may not make much sense at the moment, but hopefully it will soon.

What the Frunk?

Much of this post will make use of Frunk’s types (e.g. HCons, HNil), methods, macros (esp. for describing macro types via the Hlist! type macro), and terminology.

It might be easier to follow along if you add Frunk to your project and play around with it. Frunk is published to Crates.io, so to add it your list of dependencies, simply put this in your Cargo.toml:

1
2

[dependencies]
frunk = "${latest_version}"

Alternatively, take a look at the published Rustdocs.

Plucking from HLists

Given an HList, how can we write a function that allows us to pluck out a value by type (if the HList does not contain this type, the compiler should let us know), and also return the rest of the HList?

Suppose we call this function pluck(), it should behave like so:

1
2
3
4
5
6
7
8

// h has type Hlist![ {integer}, &str, f32, bool ]
let h = hlist![ 1, "Joe", 42f32, true ];

// We tell it the target type, and let the compiler infer the rest
let (target, remainder): (f32, _) = h.pluck();

assert_eq!(target, 42f32);
assert_eq!(remainder, hlist![1, "Joe", true]);

Implementation intuition

Our basic logic is fairly simple, given an HList and a Target type:

1. If the head of the Hlist matches the Target type, return the head of the Hlist and the tail of the Hlist as the remainder in a pair (2 element tuple)
2. Otherwise,
   1. Store the head in current_head
   2. Call pluck() again on the tail of the current Hlist with the same Target type (i.e. recursively call 1. with the tail), and store the result in (tail_target, tail_remainder) pair.
   3. Return the target plucked from the tail, and prepend current_head to the remainder from the tail. Return both in a tuple like so: (tail_target, HCons { head: current_head, tail: tail_remainder} ).

First attempt

First, let’s assume we’ll be working with a trait; call it Plucker. For now, let’s also assume that it will be parameterised with 1 type, the target type, and will also have an associated type, Remainder. There isn’t really a hard and fast rule for when you should use type parameters vs associated types, but if you’re interested, you can take a look at this Stackoverflow question because Matthieu offers some great advice.

Personally, I always try use an associated type when I need to refer to the type from somewhere else (espescially recursively; more on this later). However, going with a type parameter is useful when you need to have different implementations of a trait for the same type in different circumstances. We saw this with Add, where the right hand side was a type parameter, RHS, allowing you to declare different Add implementations for the same left-hand-side type and letting the compiler find the correct implementation to use at + call sites depending on the type of thing being added with.

1
2
3
4
5
6
7
8

// Our trait
trait Plucker<Target> {

  type Remainder;

  // Pluck should return the target type and the Remainder in a pair
  fn pluck(self) -> (Target, Self::Remainder);
}

The “exit-type” implementation is for when the current head of the HList contains the target type, so let’s jot that down that:

1
2
3
4
5
6
7
8
9

impl <Target, Tail> Plucker<Target> for HCons<Target, Tail> {

  // Target is the head element, so the Remainder type is the tail!
  type Remainder = Tail;

  fn pluck(self) -> (Target, Self::Remainder) {
    (self.head, self.tail)
  }
}

Now let’s implement the second piece; the non-trivial part where the target type is not in Head, but in the Tail of our HList. I’ll sometimes refer to this as the “work-to-be-done” type.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

impl <Target, Head, Tail> Plucker<Target> for HCons<Head, Tail>
  where Tail: Plucker<Target>

  // Target is in the tail, so we add the current head type to the remainder
  // And use the Tail's Plucker's Remainder type as the tail :)
  type Remainder = HCons<Head, <Tail as Plucker<Target>>::Remainder>;

  fn pluck(self) -> (Target, Self::Remainder) {
    let (tail_target, tail_remainder): (Target, <Tail as Plucker<Target>>::Remainder) = self.tail.pluck();
    (
      tail_target,
      HCons { head: self.head, tail: tail_remainder}
    )

  }
}

Looks good right? But if you send that to the compiler, you’ll be hit with this message:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

error[E0119]: conflicting implementations of trait `Plucker<_>` for type `frunk_core::hlist::HCons<_, _>`:
   --> tests/example.rs:306:1
    |
296 |   impl <Target, Tail> Plucker<Target> for HCons<Target, Tail> {
    |  _- starting here...
297 | |
298 | |     // Target is the head element, so the Remainder type is the tail!
299 | |     type Remainder = Tail;
300 | |
301 | |     fn pluck(self) -> (Target, Self::Remainder) {
302 | |         (self.head, self.tail)
303 | |     }
304 | | }
    | |_- ...ending here: first implementation here
305 |
306 |   impl <Target, Head, Tail> Plucker<Target> for HCons<Head, Tail>
    |   ^ conflicting implementation for `frunk_core::hlist::HCons<_, _>`

What the Rust compiler is helpfully is telling us, is that it can’t distinguish between our two implementations, and if we look closely at the types, that is indeed true:

1
2
3
4
5

// exit (work done) type implementation
impl <Target, Tail>  Plucker<Target> for HCons<Target, Tail>

// work-to-be-done implementation
impl <Target, Head, Tail> Plucker<Target> for HCons<Head, Tail>

The Plucker<Target> part is exactly the same, and sure, we’ve used Target instead of Head in the for HCons<..> part in the first case, but simply using different type parameters isn’t enough to distinguish between the two.

Furthermore, note that you can’t use the lack of constraints (or where clauses) to distinguish between implementations either. This is because the current lack of an implementation for a given type parameter doesn’t mean that it can’t be added later (see this Stackoverflow questions for more details).

Welp, back to the drawing board.

Second attempt

What we’ve learnt is that we need to have another type parameter in order to distinguish the exit-type and the work-to-be-done-type implementations, so let’s add one to Plucker. Intuitively, we know that we want to have a way to distinguish between “the target is here in the HList” (exit) and “the target is over there in the HList” (recursion), so let’s call our type parameter Index.

1
2
3
4
5
6

// the new and improved Plucker trait
trait Plucker<Target, Index> {
    type Remainder;

    fn pluck(self) -> (Target, Self::Remainder);
}

Then, let’s add a type to identify the index for the exit-type implementation. We’ll use an empty enum because we just want to have a type, and we don’t want it to be available at runtime (ensuring zero runtime cost for our type).

1
2
3
4
5
6
7
8
9
10
11
12

// This will be the type we'll use to denote that the Target is in the Head
enum Here {}

impl <Target, Tail> Plucker<Target, Here> for HCons<Target, Tail> {

  // Target type is in the Head, so the Remainder type must be the tail!
  type Remainder = Tail;

  fn pluck(self) -> (Target, Self::Remainder) {
    (self.head, self.tail)
  }
}

What about the work-to-be-done-type? Let’s imagine a scenario where we want to pluck a Target of type MagicType (let’s assume it’s declared as struct MagicType, so a type with a single element in it), and we have the following HLists to pluck() from; what would the Index be?

1. HNil

   Trick question, there is no Index because our target of MagicType isn’t here. The compiler should fail to find an instance/implementation of our trait.

2. hlist[ MagicType ] (this is syntactic sugar for HCons<MagicType, HNil>)

   Index would clearly be our Here enum type

3. hlist![ Foo, MagicType ] (this is syntactic sugar for HCons<Foo, HCons<MagicType, HNil>>)

   Index can’t be Here, but we know that in order for the compiler to be satisfied that it can reach our end-type in 1. Here needs to be somewhere inside the type, but we can’t just use it as is, otherwise we’ll run into the same “conflicting implementation” error as before. So, let’s introduce new type There<A>, that has one type parameter. In this case, the Index should resolve to There<Here> because the target type is in the head of the tail.

4. hlist![ Foo, Foo, MagicType ]

   Following from 3. Index would have to be There<There<Here>>

5. hlist![ Foo, Foo, Foo, MagicType ]

   What else could Index be but There<There<There<Here>>>

That Looks alright, so let’s give it a go. Since the new type has a type parameter but no real data to associate it with, we’ll need use the PhantomData trick (discussed in the last post).

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

// Type for representing a not-here Index
struct There<T>(PhantomData<T>);

impl<Head, Tail, Target, TailIndex> Plucker<Target, There<TailIndex>> for HCons<Head, Tail>
    // This where clause can be interpreted as "the target must be pluckable from the Tail"
    where Tail: Plucker<Target, TailIndex>
{
    type Remainder = HCons<Head, <Tail as Plucker<Target, TailIndex>>::Remainder>;

    fn pluck(self) -> (Target, Self::Remainder) {
        let (target, tail_remainder): (Target, <Tail as Plucker<Target, TailIndex>>::Remainder) =
            <Tail as Plucker<Target, TailIndex>>::pluck(self.tail);
        (target,
         HCons {
             head: self.head,
             tail: tail_remainder,
         })
    }
}

And that’s it, we’ve written implementations of Plucker for HList. The implementation for work-to-be-done type is type-recursive in its Index type as well as its Remainder associated type. The cool thing is that the compiler is in charge of figuring out what the concrete types should be at any given pluck() call-site. In fact, you can see from this example in Frunk that the compiler will also happily infer the remainder for us too.

Type-level walkthrough

Let’s take a step back and work through what we’ve done.

We’ve declared an implementation of Plucker for the trivial exit-type (Target is in the head).

We’ve also declared an implementation for the work-to-be-done type (Target is in the tail). This implementation, however, is dependent on its recursive types of Tail and TailIndex (hint: look at the where clause). Intuitively speaking, an implementation of this type only exists if the current HList’s Tail has either:

1. An implementation for the exit-type; the Target type is in the head
2. Another work-to-be-done implementation of Plucker. This ultimately means that eventually there has to be a 1. in the tail somewhere.

Let’s try to walk through a mental model of how pluck() gets associated to the proper implementation.

1
2
3
4
5
6
7

// Given an HList (type explicitly declared for clarity)
let h: Hlist![ &str, bool, f32, i32 ] = hlist![ "Joe", false, 42f32, 9 ];

// Suppose we want to get the float (f32) value out
// We're ignoring the remainder and its type (Rust will figure it out),
// because it isn't relevant for now.
let (v, _): (f32,_) = h.pluck();

We’re ignoring the remainder and its type (Rust will figure it out if we use the underscore binding _), because it isn’t relevant for what we’re about to do.

In the following steps, we’ll substitute concrete types into our implementations where possible; similar to how functions get bound to values during the substitution model of evaluation (normally used for evaluating runtime values). We’ll do this in steps, so it’s possible that in the earlier stages, we don’t quite know the concrete type yet, but we’ll go down the “stack”, and come back up and fill those types in, too, once we know them.

1. pluck() on Hlist![ &str, bool, f32, i32 ]

   Since our Target type (f32) is not in the head, it doesn’t match with the Here case, so we will try to use the work-to-be-done case (Index is There<TailIndex>) and fill in as many types as we can for now. Let’s replace some type parameters with their concrete types where possible.

   Concrete types:

   • Head → &str
   • Tail → Hlist![bool, f32, i32 ] (remember, this is syntactic sugar for HCons<bool, HCons<f32, HCons<i32, HNil>)
   • Target → f32 (this doesn’t change)
   • Remainder → Don’t know yet, but we already know that the current Head will be in it, since it isn’t the target type. And we know the tail of Remainder will be the remainder from pluck()ing f32 from the tail, so we can reference it as HCons< &str, < Hlist![bool, f32, i32] as Plucker<f32, There<Here>> >::Remainder > for now.
   • TailIndex → Don’t know yet, but we’ll find out. Let’s call reference it as TailIndex1 for now.

2. pluck() on Hlist![bool, f32, i32] (Tail from 1.)

   Again, f32 is not in the head of our type, so we know we aren’t going to be working with the exit-type typeclass implementation (e.g., Index is not Here yet.)

   Concrete types:

   • Head → bool
   • Tail → Hlist![ f32, i32 ]
   • Target → f32 (again, this doesn’t change)
   • Remainder → Still don’t know yet, but we do know that bool will be in it since it isn’t our target. Similar to the previous step, we’ll tentatively call it HCons< bool, < Hlist![ f32, i32] as Plucker<f32, Here> >::Remainder >
   • TailIndex → Don’t know yet, but let’s rename it TailIndex2 for now and fill it in later.

3. pluck() on Hlist![ f32, i32 ] (Tail from 2.)

   The head has type f32 and the target type is f32, so we’ve arrived at the exit-type implementation.

   Concrete types:

   • Head → f32
   • Tail → Hlist![ i32 ]
   • Target → f32 !
   • Remainder → Since we’ve found our target, we know that Remainder must be the tail, and thus Hlist![ i32 ], or its equivalent HCons< i32, HNil >
   • Index → Here !

Now, that we’ve finally resolved a concrete type for Index, we can go backwards up the type-level stack and fill in our unknowns:

• Step 2:
  • TailIndex2 → Here, which means that Index is There<Here>>
  • Remainder → HList![ boo, i32 ]
• Step 1:
  • TailIndex1 → There<Here>, which means that Index is There<There<Here>>>
  • Remainder → HList![ &str, boo, i32 ]

The compiler is thus able to find a trait implementation to pluck() a f32 out of an Hlist![ &str, bool, f32, i32 ] that looks like this (with all the type parameters bound to a concrete type):

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

// Remember Hlist![ ... ] is just a type-macro to make it easier to write nested Hcons
impl Plucker< f32, There<There<Here>> > for Hlist![ &str, bool, f32, i32 ]
   where Hlist![ bool, f32, i32 ]: Plucker< f32, There<Here> >
{
  type Remainder = HList![ &str, boo, i32 ];

  fn pluck(self) -> (f32, Self::Remainder) {
    let (target, tail_remainder): (f32, < Hlist![bool, f32, i32] as Plucker<f32, There<Here>> >::Remainder) =
      < Hlist![ bool, f32, i32 ] as Plucker<f32, There<Here>> >::pluck(self.tail);
    (target,
     HCons {
         head: self.head,
         tail: tail_remainder,
     })
  }
}

Whew! That took a while, but I hope it helps illustrate how you can use a mental model similar to the substitution model of evaluation, but with types, in order to prove the existence of implementations for a given type.

By the way, by default, the compiler has a limit on how many levels of recursion/expansion this search for a typeclass instance goes. In my testing, I found this to be 64 levels and verified it to be so by looking at Rust’s source code. If you hit the limit, the compiler blow up, but will helpfully offer you a solution:

1
2
3
4
5
6
7
8

error[E0275]: overflow evaluating the requirement `frunk_core::hlist::HNil: frunk_core::hlist::Plucker<bool, _>`
   --> tests/derivation_tests.rs:296:35
    |
296 |     let (e, _): (bool, _) = hello.pluck();
    |                                   ^^^^^
    |
    = note: consider adding a `#![recursion_limit="128"]` attribute to your crate
    = note: required because of the requirements on the impl of `frunk_core::hlist::Plucker<bool, frunk_core::hlist::There<_>>` for `frunk_core::hlist::HCons<bool, frunk_core::hlist::HNil>`

So, simply add #![recursion_limit="128"] to your crate. If you hit the limit again, the compiler will tell you to double the limit again. Ad infinitum.

Sculpting HLists

Great ! Now that we’ve finished with Plucker, let’s go one level deeper: making use of Plucker to do something even more interesting; sculpting HLists !

Here is the basic idea of what we want to be able to do:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

// Given an HList of type Hlist![ i32, &str, f32, bool ]
let h] = hlist![9000, "joe", 41f32, true];

// We'd like to be able to "sculpt" it into another, differently shaped HList.
//
// Of course, the types in the new HList must be a subset of the original HList,
// and if not, compilation should fail.
//
// Similar to pluck(), we'd also want the remainder of the original HList _not_
// used in the final result.
let (reshaped, remainder): (Hlist![ f32, i32, &str ], _) = h.sculpt();
assert_eq!(reshaped, hlist![41f32, 9000, "joe"]);
assert_eq!(remainder, hlist![true]);

// the following should fail to compile, because there is no char in the original Hlist
let (reshaped, _) = (Hlist![char], _) = h.sculpt();

Implementation intuition

Let’s call our trait Sculptor. We should be able to re-use our Plucker trait, which which means we’ll work with Targets and Indexs, but there’s more than one of each!

Intuitively, this is the kind of logic that we want:

Given TargetHList (target HList) and SourceHList (source HList), and assuming the types in the former is a subset (not necessarily in order though) of the latter:

1. Pluck value with the head type of TargetHList from SourceHList:
   • Store the result in a (plucked, remainder) tuple
2. Call sculpt on remainder, passing the tail type of the current TargetHList as the new TargetHList type.
   • Store the result in a (sculpted_tail, sculpted_remainder) tuple
3. Return (HCons { head: plucked, tail: sculpted_tail }, sculpted_remainder)

Note that in 1. we are making use of pluck(), and there is a recursive call to sculpt() in 2. Since there is a recursive call to sculpt(), it means that we need an exit-type as well. Intuitively, we’ll pencil one in:

When the target HList is empty (HNil), return a tuple (HNil, SourceHList)

First attempt

Given our logic, let’s assume we want 4 type parameters in our trait. Our trait is a bit more complicated than our Pluck trait, but not by much. We make use of the same associated-type trick to hold the type of Remainder to be returned as the 2nd element in our type that will be filled-in when we write instances of the trait.

1
2
3
4
5
6

trait Sculptor<Target, TargetTail, HeadIndex, TailIndices> {

  type Remainder;

  fn sculpt(self) -> (HCons<Target, TargetTail>, Self::Remainder);
}

The instance of Sculptor for the exit-type should be simple, right?:

1
2
3
4
5
6
7
8
9
10
11
12

// Our exit condition is when Target is HNil, so we don't care about the tail of the target
// nor do we really care about the type of SourceHList
impl <TargetTail, HeadIndex, TailIndices, SourceHList> Sculptor<HNil, TargetTail, HeadIndex, TailIndices> for SourceHList {

    type Remainder = Source;

    // ?!?!? HNil as the head type of an HCons doesn't make sense
    fn sculpt(self) -> (HCons<HNil, TargetTail>, Self::Remainder) {
        // nevermind
    }

}

Ooops; that didn’t work; our type signature for the trait can’t be fulfilled when implementing our instance! We simply have too many type parameters in our trait, even for the exit-type implementation (try implementing for the recursion case…it’ll become more apparent)

Back to the drawing board.

Second attempt

Let’s collapse our target-related type parameters into a single Target type parameter and our indices-related type parameters into a single Indices type parameter in our Sculptor trait declaration, and rely on the implementations to dictate (specialise) what types they should be (similar to how the Plucker trait had no mention of There or Here).

1
2
3
4
5
6

trait Sculptor<Target, Indices> {

    type Remainder;

    fn sculpt(self) -> (Target, Self::Remainder);
}

The exit-type implementation will still be when we have HNil as the target. Thinking it through further, in the case that we don’t have a HNil as the target, it’s obvious that Source can then be literally anything, so we’ll rename its type parameter Source. Since our intention for Sculptor is for Indices to be an HList of Here or There<A> (one for each type in our Target HList), the exit Indices must therefore be a valid Hlist. Since we don’t need an index to find an empty target, let’s make Indices HNil for simplicity.

1
2
3
4
5
6
7
8

impl<Source> Sculptor<HNil, HNil> for Source {
    // Since Our Target is HNil, we just return the Source
    type Remainder = Source;

    fn sculpt(self) -> (HNil, Self::Remainder) {
        (HNil, self)
    }
}

To figure out the type parameters needed for our work-to-be-done type, let’s work through the logic we laid out earlier.

At minimum, we know we’re writing an instance of Sculptor for a Source of type HList, and our Target type is also an HList, so we’ll use SHead and STail to describe the “Source” HList (so HCons<SHead, STail>), and THead and TTail to denote the “Target” HList (similarly, HCons<THead, TTail>).

1. Pluck value with the head type of TargetHList from SourceHList:
   • Store the result in a (plucked, remainder) tuple

Since we need to pluck() a THead from our Source HList, we’ll need a type parameter for the first index, so let’s name it IndexHead. In addition, in order to pluck(), we need a Plucker too, so this constraint is needed somewhere in our implementation declaration:

1

 HCons<SHead, STail>: Plucker<THead, IndexHead>

1. Call sculpt() on remainder, passing the tail type of the current TargetHList as the new TargetHList type.
   • Store the result in a (sculpted_tail, sculpted_remainder) tuple

Since we want to sculpt the remainder of calling pluck() in step 1. into type TTail (tail of TargetHList), we’ll need to have an HList of indices for that purpose too, so let’s call it IndexTail. Note that we don’t need a separate type parameter for the remainder from 1 because we can take advantage of the associated type on Plucker.

1
2
3
4
5

// In English, this is read as:
// "The remainder of plucking the Target head type (THead) out of the source HList
// must have a Sculptor implementation that lets us turn it into the tail type of
// the Target HList (TTail) using the tail of the current Indices (IndexTail)"
<HCons<SHead, STail> as Plucker<THead, IndexHead>>::Remainder: Sculptor<TTail, IndexTail>

1. Return (HCons { head: plucked, tail: sculpted_tail }, sculpted_remainder)

What will the Remainder type be? It should be the remainder of sculpting the remainder from plucking the head type (THead) out of the current source HList into TTail (yeah…)

1

type Remainder = <<HCons<SHead, STail> as Plucker<THead, IndexHead>>::Remainder as Sculptor<TTail, IndexTail>>::Remainder;

Putting all these types together with the logic, we have

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

impl <THead, TTail, SHead, STail, IndexHead, IndexTail> Sculptor<HCons<THead, TTail>, HCons<IndexHead, IndexTail>>
    for HCons<SHead, STail>
    where
        HCons<SHead, STail>: Plucker<THead, IndexHead>,
        <HCons<SHead, STail> as Plucker<THead, IndexHead>>::Remainder: Sculptor<TTail, IndexTail> {

    type Remainder = <<HCons<SHead, STail> as Plucker<THead, IndexHead>>::Remainder as Sculptor<TTail, IndexTail>>::Remainder;

    fn sculpt(self) -> (HCons<THead, TTail>, Self::Remainder) {
        let (p, r): (THead, <HCons<SHead, STail> as Plucker<THead, IndexHead>>::Remainder) = self.pluck();
        let (tail, tail_remainder): (TTail, Self::Remainder) = r.sculpt();
        (
            HCons {
                head: p,
                tail: tail
            },
            tail_remainder
        )
    }

}

As you can see, our implementations of Sculptor is type-recursive in an interesting way, and there are quite a few dependencies that need to be worked out between all the type parameters and the Plucker trait as well as the Sculptor trait itself (it appears in the where after all). Fortunately, the Rust compiler will do that for us (and if need be, tell you to raise the #![recursion_limit] in your crate).

If you’re not convinced this works, please by all means check out the hlist module in Frunk, in particular the Sculptor trait.

Conclusion

One last thing: the Plucker and Sculptor things aren’t just cute exercises; Plucker has already paid dividends when modeling Sculptor, and Sculptor, well, it’s instrumental in letting us do cool stuff like convert between structs with different LabelledGeneric implementations (to an extent, anyways), and other, even cooler generic functions. We’ll talk more about this in another post.

If you do a search, you’ll find a number of articles on the Interwebs that introduce Rust’s trait system, but not many that go deep into how to use it when you need to do non-trivial type-level recursion in your trait implementations (though how often this need arises is … another topic altogether). I also find that people generally don’t talk about what they did wrong, so I wanted to share my failed approaches as well.

The goal of this post is to hopefully help others who are curious, or have a need to do something similar, as well as to leave notes for myself in case I ever need to revisit this in the future. The mental models for breaking down the problem, defining types, and building up to an implementation might not work for everyone, but they’ve helped me.

Personally, I think it’s awesome that a close-to-the-metal systems programming language like Rust has a powerful enough compiler and type-system to allow for these kinds of techniques. As you can see, we’ve managed to build powerful, reusable abstractions without doing anything unsafe, and we’ve exposed an API that requires just the bare minimum of type annotations; Rust infers the rest :) In any case, I hope this post was useful, and as usual, please chime in with questions and suggestions.

Credit

1. The Here and There<A> design was largely gleaned from this code. I stand on the shoulders of giants :)

** It goes without saying that these operations need to be type-safe. That is, they are verified by the compiler without using any unsafe tricks that could blow up at runtime.